Comparative Indoor Covid-19 Transmission Risks

Ever since the lockdowns started--and before, actually--I've been trying to understand what activities involve the most risk of transmitting Covid-19.  Obviously, when looking to reopen, we have to balance out the economic benefit of a particular activity versus its risk of driving infection rates higher.  We still do not, however, have definitive answers on exactly which activities entail the highest risk.  Each state which introduced measures to control disease spread took a variety of actions, and usually at a very compressed timeline so that it is impossible to definitively say which measures specifically are responsible for how much of the decreased disease transmission that followed.

Unfortunately, this situation is likely to continue given that places that are reopening are also tending to gradually reopen activities across the board in a phased, rather than pick specific targeted activities at specific phases to reopen fully.  So we are again probably going to end up with ambiguous data on what activities are the most useful to curtail.

Crowded, Static, Indoor Settings--Particularly Risky?

My intuition currently is that may be one clear, standout activity type that has the most impact on transmission spread: namely, crowded indoor gatherings.  This is an obvious danger, to be sure, but how much more dangerous this type of activity is than other activities has been frustratingly difficult to quantify.  We have some various studies on respiratory droplet spread among groups, and some studies on the distance the virus might be able to spread via air convection currents in enclosed spaces . . . but not a lot, really.

The best cases I've seen so far that indoor close quarters are the big danger have been made by case studies.  I'm pretty convinced by Dr. Erin Bromage's post on this: https://www.erinbromage.com/post/the-risks-know-them-avoid-them .   I highly recommend reading this blog post in full; he discusses some of the most significant instances of "super spreading" and tries to draw out what each of them have in common.

A Slightly Different Take on the Question

I wanted to add a little bit to this conversation by trying to look at indoor risk in a different way.  I want to compare two indoor activities which might not seem tremendously different at first, and I want to try to roughly quantify the different risk involved in them using imaginative but numerical reconstruction.

This is going to be similar to a type of exercise called a "Fermi Problem" in physics (https://en.wikipedia.org/wiki/Fermi_problem).  The idea is to get to an idea of comparative risk between two different activities, to maybe within an order of magnitude.  I think this is a useful exercise because it can give you a framework for trying to guess at comparative risk, and maybe do better with the guessing than simple intuition.

So here's one situation: imagine you are observing a grocery self-checkout kiosk.  One person is checking out and he coughs.  Five minutes later, he is gone and another person is checking out in the same space.  Another five minutes later, and another person checks out in the same space.  What are the chances that you have observed a transmission of the disease?

Let's answer this question by making up a measure of risk we'll call a "risk factor".  The number will be arbitrary, but we'll pick a baseline: being in the immediate vicinity of an infected person who coughs.  When one person emits infected droplets into a particular space, that space is contaminated and anyone in the immediate vicinity is at a certain risk.  But then time becomes a factor, because the infected droplets instantly begin to fall and to disperse, and so the amount of contamination in that space immediately begins to drop.  So we need to make the risk factor correspondingly drop over time for people who pass through later.

And so the risk for our self-checkout kiosk scenario is going to be the baseline risk--let's call it a 3 for the first five minutes of exposure--but then reduced over time.  We'll guess that after five minutes, the next five minutes would give you a risk factor of 2, and then the next five minutes would be 1, and then zero thereafter.

In the scenario we have just described, the total risk factor for the transmission of the disease is therefore 3 "risk units": 2 for the first person and 1 for the second.  How often would this happen in a day?  Let's guess a hundred times in a single day, which means that the combined risk for a day at the self-checkout kiosks is 300.

Change the Scenario

Now let's take that baseline "cough", and instead think about when it happens during a religious ceremony which lasts one hour.

First, the person who is the source of the cough is no longer merely passing through the space.  So if there was one cough at the self-checkout kiosk at which the person spent 5 minutes, there will now be 12 coughs by that same person over the course of the hour.  

Then, every person who is next to the coughing person will *also* be stuck in place, and thus have immediate exposure--for each cough--for the first five minutes, which we said would count for the full baseline 3 risk units, but then also exposure for the next five minutes, which we said was 2, and also the next five minutes, which we said was 1.  So, 6 risk units total per person, per cough.  

But *furthermore*, rather than just two people total exposed, the contamination occurs inside a sea of people.  There are now at least two people to the right within infection range, and two people to the left, and probably three people in front and a person behind.  Furthermore, given a closed, recirculating air system, the particles can drift all over the place and find a person in any pew to which it drifts.  Easily a dozen people or more could be exposed each time.

And why are we just counting coughing, anyway?  Loud speaking emits just about as many droplets as coughing.  Singing emits *more* droplets.  So what do congregational responses and hymn singing do to the risk factor, remembering that it's not just a few people coughing but everybody, and all at once?  Depends on the type of congregation, but I'd say you should multiply the risk by at least a factor of 10 here, and this is probably an understatement.

So if there are just 12 coughing people in the entire congregation, instead of the 100 we figured for the grocery story, the risk factor is now 12 * 12 * 6 * 12 * 10, which is 103,680. We're at over 300 times more risky for the hour of worship than for a day of checking out groceries.

Conclusion

So what's the conclusion of this kind of guesswork?

First, I'm convinced that this sort of exercise is worth going through when evaluating activities for disease transmission risks.  I think if you asked a random person which activity was more of a risk of disease transmission, most people would have guessed that the religious event was the more risky.  However, if you then asked the person to guess *how* much riskier the activity was, I think they might say something like "twice as risky" or maybe even "10 times as risky".  I think hardly anyone would go so far as to say "300 times as risky" based purely on gut instinct--but this is a problem with instinct.

Numeric imagination tends to be constrained by day-to-day experiences, and in the ordinary course of events we rarely have to care about things that have a difference of magnitude that's greater than a factor of 10. 

I think this poor skill in numerical estimation doesn't matter most of the time, but can constitute a fatal mistake when it's genuinely important.  So I would recommend that everyone start playing these kinds of estimation games with themselves.  Gut instinct can be trained, and over time your intuition for these types of things can be greatly improved.

Second, although I admit my actual numbers are extreme guesswork, I actually believe in their rough correctness--I think I was actually fairly conservative.  I think static, crowded indoor events are very risky and should be treated with extreme caution just right now.

When Averages Lie

A researcher Lyman Stone has written a paper (here: https://www.thepublicdiscourse.com/2020/04/62572/) claiming to prove, by various means, that lockdowns don't work.  Specifically, it claims that while various social measures taken to limit Covid-19 may have been successful in limiting the spread of the disease, the more extreme measures such as generalized stay-at-home orders have not been what have done the trick.

There are various reasons advanced for this argument in the paper.  Here I am only going to focus on one: Stone claims that the average time from illness onset to death for Covid-19 is well established, and that it is 20 days.  When you look at the change in death rates that occurred in many countries after establishing serious lock-down measures, however, you will see that death rates often leveled off sometime around 10 days after the more serious measures were taken.  It is impossible for the slowdown in deaths to have been caused by the lockdowns, argues Stone, because decreases in infection rates can only show up in the death counts a minimum of 20 days later.

How does Stone come up with this 20 day limit?  20 days is the average incubation time for Covid-19 (well-established at about 5 days), plus the average time from onset-of-symptoms till death, which Stone says is 15 days.

Stone's argument that lockdowns could not have caused the decrease in deaths we are seeing is summarized in the following graphic:

(original image here: https://www.thepublicdiscourse.com/wp-content/uploads/2020/04/Fig_1.png)

Why an Average Isn't Appropriate Here

To see what's wrong with Stone's argument, you need to understand what can be concealed by a simple average.  Obviously, just because the average time to die after infection is somewhere around 20 days, that doesn't mean death happens exactly 20 days after infection.  There will be some range of timelines here: some people will die more quickly than average and some people will die more slowly than average.  If enough people die more quickly than the average, then perhaps you would expect to see an effect on the death rates.  The question then becomes, given the average timeline reported by Stone is correct, how many people would need to die faster than average in order for the lockdowns to cause the death rate changes we see at these earlier dates?

Stone does seem to give some amount of thought to this.  He links to several studies on death rates from Covid-19 and he does say that there are a range of days-to-death numbers, which he says is "twelve to twenty-four" days.  With the addition of the days for incubation (which he says is 2-10), this still makes it impossible for the lockdowns to be having an effect on the death rates as early as 10 days

But Stone's claim of a range of "twelve to twenty-four" days is incorrect.

What is the Actual Distribution of Days-to-Death?

Stone linked to several studies to support his claim of a 12-24 day onset-of-symptoms-to-death number.  I think his range must be something like an amalgamation of the averages from these several studies, because none of the studies actually present a range of days-to-death that match the claim.  For example, here is the distribution of days-to-death after onset of symptoms from one of the studies done on the Chinese data:

The article is here: https://www.thelancet.com/journals/laninf/article/PIIS1473-3099(20)30243-7/fulltext .   I produced the graph from the raw data, which is available here: https://github.com/mrc-ide/COVID19_CFR_submission .  I've also created a hand-entered range of probabilities as a data series that matches this distribution (for reasons I'll get into later) which looks like this:

You can see that the range of possible days-to-death here is far wider than Stone initially reported.  They go from as short a time as 5 days to as long as 41 days.  Furthermore, the data is clearly asymmetrical: it is heavily weighted to the left-hand side.  There is a very clear peak at 11 and 12 days and then a "long tail" with some people lingering on for many days before succumbing.  This pattern holds up pretty well in subsequent studies.

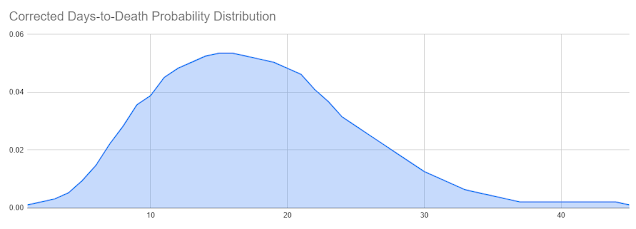
This same study produced a corrected probability curve from the data it collected, which I've reproduced as a series:

This distribution is shifted slightly to the right compared to the raw data, which the authors explain as a correction for the timing of the data collection.  The original distribution was weighted to the earlier deaths because it represented a sample taken when the epidemic was still in progress, thus cutting off deaths that occurred on a longer time frame.  This is an important point I'll return to later.

For now, it should be noticed that although the peak of this curve is right around the 15-16 day mark (which sort of agrees with Stone's chosen average number), it still has a leftward trend and it still covers a much wider range of possibilities than the "12-24" range Stone was proposing.

However, this curve does have a peak right around 15 days, and in fact its average is even longer than 15 days: it's 17.8 days rather than 15, because the long tail on the right has a disproportionate effect on the average.  So if the curve has an average of greater than 15 days, and it has a clear peak at around 15 days, isn't it safe to take these 15 days, plus 5 for the incubation time period, as a minimum time before you should expect to see a clear change in the death rates chart?  Certainly it doesn't seem as if you should see much of an effect by just 10 days, as only about 15% of all deaths in this distribution happen at 10 days after symptoms begin or earlier and only 2% of all deaths happen at 5 days or earlier (recalling that incubation itself is an average of 5 days).

Getting an Answer from a Model

There are deterministic ways to calculate how a curve of the above sort should impact a death rate chart.  Those involve some difficult math, however, and it's easy to make mistakes doing that (at least, it is for me).  Another way to get the same answer is to use an epidemic model.  Now, modeling is something about which a lot of people have expressed a great deal of doubt and distrust.  I think there is a lot of misunderstanding about where models are appropriate and where they are not, and when they can be trusted and when they cannot, so this is a good opportunity to discuss how models can be used well.

Here, an epidemic simulation model can be very useful because we have a very specific question we want to ask: is it possible that we could see noticeable changes to the daily death graph as early as 10 days or so, with a disease incubation of 2-8 days (average of 5) and a days-to-death distribution that matches the observed, corrected distribution for Covid-19: that is, with an average of 17.8 days-to-death and a slight bias to lower values and a long tail?  If we applied these parameters to a SIR-based epidemic simulation and we saw only a 10 day delay between the start of some intervention and a clear signal on the graph, then this would disprove Stone's argument.    He claims that it is not possible for an intervention to produce noticeable results on the daily death graph so soon because the average days-to-death is too far in the future.  The existence of a system, even artificial, in which such an intervention does produce a noticeable result in that short time period would be proof against this, because even if the artificial system does not represent reality in many ways, we can construct it in such a way that Stone's point about average days-to-death would affect it just as much as it would affect a real system.

Please notice the very careful way I constructed the previous sentence. It is very crucial, when using model systems, to understand in what ways they represent reality and in what ways they don't--otherwise, the results of a model output can be over-interpreted.  In this particular case, it is very easy to construct a reasonable model in which if Stone's argument about average days-to-death being too long were true, the model would also be affected.  I did so, and the details of the model are as follows:

Details of the Model

I first generated a standard SIR model using a Python package called "Epydemic".  This particular model starts with a random network of individuals with a range of connectedness designed to approximate the mix of more sociable and less sociable members of actual society.  Then it starts with a certain seed of infected individuals and stochastically advances the disease across the network.  Uninfected Individuals connected to infected individuals have a certain chance to become infected every day and infected individuals will become removed from the infection pool at a certain fixed rate.

I took the standard code and then modified it to produce a death rate chart.  I took the corrected days-to-death distribution curve and used it as an input: any time an individual became infected, I would randomly select a days-till-death for that individual based on the probabilities of that distribution curve (for those individuals that I selected to die based off of a set Infection Fatality Ratio).  The actual date of death was calculated for each individual who died as the date of infection plus a certain number of days for incubation (randomly selected from a symmetrical bell-curve distribution with an average of 5 days), plus a certain number of days chosen from the days-till-death distribution curve.  The average days from infection till death was therefore 23.8.

Then I coded in two interventions that I could trigger: a lesser intervention on day 17 of the epidemic and a more severe one on day 20.  These interventions would reduce the percent chance for individual infections to spread, and then I should be able to see what effect that had on the daily death rates, and how quickly these effects were noticeable.

Results

I ran this for a population of 50,000 (chosen for practical reasons of computational speed) first with no intervention and got a fairly standard epidemic curve for an uncontrolled, highly infectious disease:

Notice that you can see how the deaths trail off more slowly than they ramp up, which I think is due to the "long tail" of the days-to-death probability distribution.

Then I applied an intervention which lowered the probability of infection for any given individual on the graph.  I started with a small intervention on day 17 of epidemic which reduced the percent chance of infection by 1/3.  This is the equivalent of an intervention that changes the R from something like 3 to something closer to 2, and it was intended to model the hypothetical situation in which early, less-than-lockdown measures taken did not have the capability to drastically flatten the curve on their own.  This produced this output:

Lowering the infection rate by 1/3rd had a noticeable impact on the total deaths but is hard to pinpoint on the graph, which is as expected.

Then I added a more drastic intervention on day 20, so that from that point on, new infections were cut by a total of 80%, the equivalent of lowering the R to about 0.6.  Note that this intervention only effected numbers of infections.  It could only affect the death rate chart after the delay of incubation plus days-to-death had been met.  In order to also see what happened if the interventions were removed, I turned off the infection suppression at day 50.  The results were as follows:

Even though the average days from infection until death was 23.8 days for this simulation, the timeline for dramatic changes being clearly noticeable on the chart is far less.  Both when beginning interventions and in ending interventions, results were clearly noticeable within about 10 days of the major intervention.  The exact boundaries are obscured because the simulation is stochastic and therefore has lots of random spikes and dips, but I ran the simulation a number of times and got fairly consistent results back.  (Sorry, I didn't save results from multiple runs to create an average of runs with ranges.)

Why Does This Happen?

The obvious question now is, why?  How is it that a clear effect can be seen so far before the average time-to-death is reached?  To explain this, recall the correction to the days-to-death distribution that had to be made earlier.  The actual distribution of deaths measured in the study from which my curve was derived was even further biased to the left and looked like this:

This matches the actual distribution of onset-to-death times seen during the epidemic outbreak.  While the outbreak is going on, not everyone who will die from the infection has yet died from the infection, which means faster deaths make up a disproportionate amount of the death curve than slower deaths.  When the distribution is already slightly weighted to the left, this additional skewing factor creates a very clear earlier signal.

I had constructed the above synthetic curve to have exactly the same weighted average value as the corrected curve (17.8 days till death).  To be honest, this was done as a mistake because I initially thought I should be replicating the observed days-to-death distribution from the study rather than using the timeline corrected version.  But since I had created this distribution and it had the same average value as the correct one, I decided to do some runs with that distribution to see what would happen.  I saw a very clear earlier signal in the graphs produced by these simulations, by about 3-5 days.  Here's an example which shows a very clear result by day 27 or so:

This shows quite conclusively that it is the shape of the distribution, and not just its average, that has a definite effect on how soon you can see results from an intervention.  

Conclusion: How Long Should We Wait to Evaluate an Intervention?

At this point I want to reiterate what I said earlier about models: we should be careful of what conclusions we allow ourselves to draw from their output.  Because we have created synthetic situations in which interventions have a clear effect within 10 days of their introduction, even though the average time between infection and death is set to 23.8 days, we have definitively disproven Stone's argument that these interventions can not be responsible for death rate changes.  But to say that we now know that the expected time between an intervention and a change in death rates is 10 days would be to overstate the results of these models.  We don't know how well this simple model actually maps to reality.  I think that the results are highly suggestive of a 10 day lag between policy change and visible results, but that's as far as we should take this conclusion.

The lesson that you should not do your calculations simply from averages, though, is absolutely clear and it represents a major mistake in Stone's original thought.

Postscript: Stone's Correction

After I began this post, Stone was corrected on his use of a simple average by a statistician named Cheianov, and produced a backup-argument that even if you model an expected peak in deaths due to lockdowns being very effective, the peaks in death rates in the real world were still off of the model slightly, by about three days.  His new argument is here: https://twitter.com/lymanstoneky/status/1253304661475385345

To this I would respond two things:

1. Quibbling over three days is unwise when there are many factors that could have a confounding effect on how accurate the models are.  In particular, this whole conversation so far has been assuming a days-to-death distribution established by some of the earliest published studies--which in turn were all constructed using data from China.  We know that Western countries have a significantly larger portion of vulnerable elderly than China does; it's quite possible that these people die more rapidly than natively healthier people.  This alone could be responsible for a left-ward bias in specifically Western death rates; we don't know.  So I think Stone's new conclusion is very weak.
2. In Stone's corrected argument, he models the "lockdowns are what's effective" hypothesis with a curve that represents only the effect of the lockdown.  In my simulations, I modeled a 3-day-earlier, not-very-effective-measure followed rapidly by a much more effective measure.  I think my approach is the more fair, since no one is claiming that only the lockdowns had any effect, just that they were the definitive change; Stone's corrected argument is therefore a mathematical strawman.  Furthermore, I did test out my models with and without that earlier 3 day intervention and it did make a noticeable difference, so this isn't just a quibble.

Overall, though, I would like to concede an important point: it is not abundantly clear from the data I've been looking at here that the lockdowns specifically must be responsible for taming infection rates.  In reality, there is too little time between when most nations started implementing lesser measures and when they changed course and opted for strict lockdowns.  The real-world data has too much variability and confounding factors to be able to differentiate yet which set of measures or which societal responses (Stone's social distancing metrics from Google, for example) had the most effect.  To illustrate this, I ran my simulation one more time with the intervention on day 17 decreasing the infection rates by a full 70% and the intervention on day 20 only bumping that up by an extra 10%.  The end result was not easy to distinguish, at all, from any of my previous runs:

This means that none of us should be too confident in our causal conclusions yet.

[EDIT: 5/11/2020]

I realized a couple of things after I posted this originally.  First, I should really provide a link for the code I'm using to create these graphs.  It's here: https://github.com/cshunk/EpydemicTest .  Warning: not pretty, though it is also quite simple.

Second, I realized that in explaining how the graph of daily deaths is biased at different times in the epidemic to earlier deaths, the obvious thing to do would have been to track what the average days-to-death was for every day in the epidemic.  I did that for a run and the result is as follows.  The orange series is what the average days-to-death was over every death that happened on that particular day:

You can see how the average days-to-death is lower earlier in the epidemic, and also drops after interventions are stopped and the disease is progressing exponentially again.  This is because as long as the number of deaths are rising quickly, recently infected people are always a larger group than less recently infected people, meaning that earlier deaths from the recently infected will still be larger than later deaths from less recently infected, even though the percentages are still small.

Understanding the Relationship between R, Herd Immunity, and Attack Rate

The end goal for dealing with Covid-19 is either complete elimination (unlikely at this point) or "herd immunity", which is the state wherein enough people are immune to the disease (either through already having had it or through a vaccine) so that the disease can no longer easily spread through the population.

How many people need to be immune in order for us to achieve herd immunity?  This is an important question for policy decisions because--given that some relatively fixed percentage of people who get the disease will die*--the answer to this question will also answer the question of how many people will need to die if you want to achieve herd immunity to a disease without having a vaccine.

It turns out that the number of people you need to achieve herd immunity is directly related to the speed at which the virus naturally propagates through your population: the basic reproduction number, or the now-infamous "R".  This can actually be shown to be the case with a little bit of thought and not much math.

Setup for the Thought Experiment

R is simply defined as the number of people that one infected person, on average, will pass the disease to for the complete time during which he is infected. Now this average number will obviously depend on two things: how naturally infectious the disease is, and how many occasions an average person in a society will have the opportunity to infect some other person.

In the middle of a pandemic, which many societal measures in place to prevent the spread of the disease and with many people voluntarily altering their behaviors so that they don't spread the disease, R is going to depend on a lot of situationally specific factors: what are the local societal restrictions, how compliant the public is with them, how have people changed their behavior due to the disease, etc.  

However, if we're talking about herd immunity, we can kind of ignore those factors, because what we are trying to get at is the percentage of the population who need to be immune in order for the disease to die away without artificially imposed behavioral changes.  In other words, what we want to know is, when can life go back to normal without fear of infection?

Infection Spread in Normal Societal Conditions

So for our purposes now, we can assume normal societal mixing in our thought experiment as a constant.  The number of people who will be infected by a single infected case, or R, is then going to depend only on how infectious the disease is, and not on abnormal societal factors.

Now, as we said, R is a value that combines the factors of how naturally infectious the disease is and how much social mixing an infected person will do during the course of the disease.  You can think of this as multiplying two numbers:  an infected person will come into close enough contact with a certain number of people during the course of the infection, and each time will have a certain percent chance to infect that person.  Multiply those two numbers and that's the total number of people whom that person will infect.  

So if an average person in a society comes into close contact with 100 people during the course of his illness and has a 2% chance of infecting someone each time, he will on average infect 2 people in total and the R of the disease will therefore be 2.

How Immunity Changes the Picture

What if, in the same scenario above, an infected person comes into contact with 100 people, but 10% of those people have already had the illness and are now immune?  Well, in that case that same 2% chance of each person getting infected will only apply to 90 out of the 100 people the infected person meets.  So that means that the R is going to drop down to 1.8.  Another way of saying this is that the baseline R of the disease (the R(0) or "R naught") needs to be multiplied by the fraction of the population that is susceptible to the disease (0.9 in our example) in order to get the current effective R value.

Now it's obvious that in order for a disease to grow in a population, R must be higher than 1.  If it's less than 1, it will begin decreasing in the population.  It can still spread if R is less than 1, but it cannot grow.  That is, if there are 1000 infected people in your population and the R is 0.7, 700 additional people will be infected in the next disease "generation", and then 490, and so on and so forth.  But as long as the R is less than 1, the disease will be progressively dying and not growing. And this is what you want from herd immunity.

**Therefore, the point at which you can claim herd immunity is exactly the point at which the fraction of people who are still susceptible to the disease would multiply with the R(0) of the disease to equal 1.**

So for measles, which has a ferocious R(0) of about 10, you would need a very low 10% of your population to be susceptible in order to reduce the R to 1, which means that you don't get herd immunity until 90% of the population is immune.  Seasonal flu, on the other hand has an R(0) of something like 1.3.  1/1.3 is around 0.77, so you can get herd immunity against the current seasonal flu with just 23% of the population already having been infected (or otherwise immunized).

Covid-19 has a very high R relative to the flu.  Estimates started at around 2.4, but have gone up with better analysis and is probably closer to 3.8.  Supposing it is 3.8, what percentage of population would need to be infected in order to confer herd immunity? 1/3.8 is about 0.26, so that means the answer is about 74% of the population.

Relationship to Attack Rate

The "attack rate" of a disease is the total percent of the population that will get the disease before it runs its course.  From a policy standpoint, it would be good to know what this number will be if we pursue achieving herd immunity via letting the infection run its course.

This total number of infected is not equivalent to the percentage of the population required to be immune in order to achieve herd immunity.  This is because even when you achieve this number--if you achieve it by letting people get infected--at that time you still have a certain percentage of people infected with the disease, and (as we said) the disease will still spread from those infected people at ever decreasing rates as it is dying out.

You can actually calculate the likely number of people who are still going to get the disease in this situation, but this is not so simple as what we have done so far: it requires differential calculus, and I said there wasn't going to be much math.  So I'll skip that part and just say: there will be some further infections after herd immunity is reached, if it is reached by lots of people getting infected.

Conclusion

Reaching herd immunity is not the same for every disease.  The number of people who need to be immune in order for herd immunity to work depends on the native infectiousness of the disease.  Because Covid-19 is quite a bit more infectious than the seasonal flu, we need to understand that getting to herd immunity with Covid-19 involves a far larger percentage of the population getting sick than is typical for a bad flu season, around 75% at a bare minimum.

-------
* Note: I said above that the number of people who will die from the disease is a relatively fixed proportion of the total attack rate.  I should acknowledge that this is not a completely safe assumption, given that various treatments could be developed or discovered that would make Covid-19 less fatal.